Application of Band Interval Selection of LED Light Sources in Color Vision

Introduction

Color vision system is an important part of quality online inspection. It has a wide range of applications in textiles, food, plastic products and some industrial inspections. In many online detection applications, when the image background has multiple colors and is relatively cluttered, it is likely that the detection target will be difficult to distinguish.

The resolution between the background and the background becomes very small [1, 2]. Scribner [3] and so on use two or more infrared bands to blend into a color image to distinguish between the target and the background surface. For color vision systems, the color signal is mainly affected by the reflection function of the surface of the object and the spectral energy distribution of the light source before imaging [4]. Choosing the right source band improves the resolution of the detection surface and simplifies the visual inspection algorithm.

The partial least squares (PLS) method is often used for the selection of a single band [5~7] or band spacing [8~10]. Many papers describe their algorithms and applications [11~13]. Elmas ry [6] et al. studied the PLS algorithm and stepwise discriminant method to select the effective band to distinguish the injured part from the normal apple surface. Hyperspectral imaging techniques are often used to select the optimal band, but for some industrial automated inspections, the system is too expensive. With the development of LED technology, there are more and more types of LED bands, and its brightness and band are more suitable for industrial automatic detection applications. However, LEDs do not provide a single band and generally have a certain band range. Therefore, this paper applies PLS analysis to study the selection of the source band spacing. Band spacing, in other words, picking the most efficient band group. Based on the PLS model, the study of band spacing is as follows: boo tstrap VIP method [8], interval partial least squares regression [9], boo tstrap method in partial least squares regression [10].

In this paper, the surface with multiple colors is selected as the experimental object, in order to distinguish and improve the resolution at the same time, select the appropriate light source band interval. Firstly, the reflection function of each surface is calibrated, then each surface type and reflection function are modeled by partial least squares method. The threshold value VIP > 1 0 is used as the basis for selecting the interval of the light source band. The selected band spacing was used as the LED band of the light source used in the experiment, and the validity of the selected band was verified experimentally.

1 color vision system

The color vision system used in the experiment consists of three parts: (1) IMprex color CCD (IPX-2M30-GCCI), standard lens LM35HC; (2) optional band LED light source; (3) sample placement table. The camera has a resolution of 1 600X1200 pixels and a spectral range of 400 to 1 000 nm. The LED light source adopts the indirect illumination mode, and the high diffuse reflectivity hemispherical inner surface uniformly reflects the light emitted from the LED array onto the detection plane, thereby obtaining better color mixing effect and uniformity.

2 mathematical model

The color picture is the characteristics of the object itself, the angle of the incident light source and the light source, and the spectral characteristics of the color CCD camera are complex [14]. The continuous spectrum can be replaced by some equidistantly spaced points. Limited by the instrument, take a point every 4 nm, the RGB value of the picture ρi = ( ri , gi , bi ) T can be obtained from

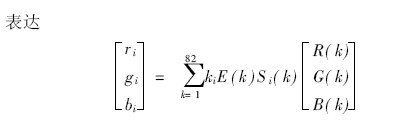
Where (R(k), G(k), B(k)) is the spectral response function of the camera, which can be determined by the camera, E(k) is the spectral distribution of the source, and S i (k) is the surface reflection of the pixel i of the object rate. Therefore, the ρi = ( ri , gi , bi ) T acquired by the camera is closely related to the reflection function of the surface of the object. The reflection functions of the different surfaces constitute the independent variable Ssurfa ce , and all surfaces constitute the dependent variable N surface . The partial least squares method is used for the analysis of the band selection, and a mathematical model is established between the independent variable X (Nsurfa ce XK interv als ) and the dependent variable Y (N surface X 1). X and Y can be expressed as

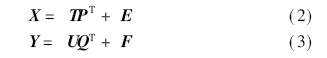
Where T and U are the scoring matrices of X and Y, respectively, and P and Q are the load matrices of X and Y, respectively. Y is a column vector, so Q is a unit vector. E and F are the residuals of the matrix. The main components T1 and U1 extracted from the two sets of variables, the PLS decomposition method is to make the covariance between T1 and U1 the maximum, which can be expressed as [11]

Where Y is the predicted value and β is the regression coefficient. In the PLS model, the VIP (importance of variables in the projection direction) score is often used as the basis for band selection, reflecting the importance of each band to the surface type Y. The VIP score on the kth band interval can be expressed by the following formula [15]

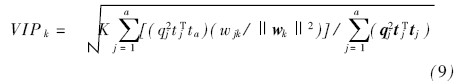
Where j = 1, 2, #, a, K is the number of band intervals, wj k is the weight of the kth band and the jth PLS factor, and tj, wj and qj are the numbers of T, W and Q, respectively j Column column vector. Band spacing with a high VI P score is considered to be more related to surface type Y. The band spacing of VIP > 1.0 is highly correlated, 0 8

3 Calibration of the reflection function

From the above analysis, the reflection function of the surface of the object is very important for PLS modeling. Therefore, the contrast function was used to calibrate the reflection function of the surface of the object using four standard diffuse reflectors with different reflectivities on a PR655 Spectroradiometer (Pho to Research Inc). The reflectance of standard diffuse reflectors is: 99% (R99), 80% (R80), 60% (R60), 40% (R40) (Spectr alo n, Labspher e Inc, No rth Sutton NH, USA). The calibrated source uses a D65 standard source. Figure 1(a) shows the reflection function of a blue target based on four diffuse reflectors.

As can be seen from Figure 1(a), there are significant differences between the four results.

Calibration is very necessary. The reflection calibration equation used in this paper can be expressed as

Where R(λ) is a function after calibration, R40 (λ), R60(λ), R80(λ) and R99(λ) are the reflection functions obtained with R40, R60, R80 and R99 standard reflectors, respectively, k1 , k2 , k 3 and k4 are the respective correlation coefficients, respectively, determined by the respective variances. Figure 1(b) shows the reflection function of the blue target after calibration. Figure 2(a) shows the color patches with multiple colors for later analysis. Figure 2(b) shows the reflection function after calibration of all surfaces on the patch.

4 Results and analysis

4 1 Band selection of the light source

As can be seen from the surface reflection functions of Figure 2(b), to distinguish any two target surfaces, there are many optional bands. But to distinguish all the target surfaces at the same time, it is necessary to select the band. Therefore, this paper applies partial least squares method to select the appropriate band as the light source, and at the same time distinguish and improve the resolution of each surface. The PLS model was constructed with the reflection function as the independent variable and each surface type as the dependent variable. Table 1 shows the effect of different PLS factors on band selection for band spacings of 4 and 8 nm.

It can be seen from Table 1 that when the appropriate number of PLS ​​factors are selected, the number of optional bands tends to be stable; at the same time, too many PLS factors will bring errors. Finally, when the band spacing is 4 and 8 nm, the PLS factors are chosen to be 15 and 8, respectively. Figures 3(a) and (b) show the inter-band interval VIP scores derived from the PLS model, respectively.

The VIP score of the 4 nm band interval and the 8 nm band interval is an important basis for selecting the appropriate band. Based on the results shown in Figure 3, in the two cases at 4 and 8 nm intervals, the three band intervals of 412~424, 480~492 and 620~628 nm have higher VIP scores. In order to determine the usefulness of these three selected band spacings, this paper uses principal component analysis to verify the importance of these three bands.

The cumulative contribution rate of the first two principal components was 94.01%, of which PC1 was 59.2% and PC2 was 34.89%. Figure 4 shows the results of principal component analysis. It can be seen that X 3 (620~ 628 nm) can better distinguish the pink surface from other surfaces. X 1 ( 412 ~ 424 nm) and X 2 (480 ~ 492 nm) can better distinguish between green surface, yellow surface, blue surface and dark blue surface.

4 2 experiment

In order to verify the effectiveness of the above method, this paper selects the LEDs containing the three selected optimal bands as the light source for experiments. The spectral band is shown in Figure 5.

Figure 6(a) shows an image obtained using the 620~628 nm band LED as the light source. It can be seen that the pink surface is well distinguished from the other four surfaces. Figure 6(b) shows the image of a 480~ 492 nm LED and a 412~424 nm LED hybrid source. It can be seen that these two bands have a better effect on distinguishing the green surface, the yellow surface, the blue surface and the dark blue surface. However, the distinction between the dark blue surface and the pink surface is poor. It is basically consistent with the theoretical analysis of the previous section. The images were collected using two light sources for comparison. Figure 6(c) shows the images collected by the LEDs of 620~628, 480~492 and 412~424 nm. Figure 6(d) shows ordinary white light illumination without a precise selection of LED band mixes.

The resolution between any two surfaces is determined by the average color difference in the CIE 1976 L* a* b* color space. Table 2 compares the average color difference of the pictures obtained by the ordinary LED light illumination selected by the method of this paper and the ordinary white light illumination mixed with the unselected LED bands. It can be seen that some unselected white light illumination has poor resolution on some surfaces, such as pink and mazarine surfaces. Any two surfaces obtained by optimal LED band illumination can be better distinguished, the resolution is higher, and the resolution of most surfaces is improved.

Edit: Sophy