[High-tech lecture hall] Analysis of LED light effect or luminous flux 1+1<2 theory

Old drivers in the LED industry should know about LEDs. When multiple LEDs are lit together, their total luminous flux is less than the sum of the luminous efficacy or luminous flux of a single LED.

That is, we often say that the luminous efficacy or luminous flux of an LED is not a relationship of 1+1=2, but a relationship of 1+1<2. The following is a brief introduction to the personal understanding of LED light efficiency or luminous flux 1+1<2 theory.

Light, as a special substance in nature, also has a special property, that is, light has "wave-particle duality", what is the wave-particle duality of light? The wave-particle duality of light is simply that light has both wave characteristics and particle characteristics.

Scientists have discovered that light can travel forward like a wave, sometimes showing the characteristics of particles. Therefore, we call the light "wave-particle duality".

Is it only light that has wave-particle duality? The guide that scientists give us is that all microscopic particles have wave-particle duality, but the difference in performance.

Solid materials like those common in our daily life are mainly characterized by particle nature, while substances like sound are mainly characterized by volatility. The reason why light is special is because it can be expressed as volatility and particle.

LED light effect or luminous flux 1+1<2 theory is actually a superposition problem of light, that is, the superposition problem of waves. Below we use the volatility of light, taking the simplest wave as an example to see how the waves are superimposed. For example, the amplitudes are A1 and A2, the vibration direction is the same, and the waves with constant phase difference are interfering with each other during the propagation process. If the vibrations of the two waves are the same, then A1=A2=A, then the wave A1 The wave equation of A2 is: A1=A2=ACOS(ωt) (where ω is the angular frequency and t is the vibration period)

The wave equations in which the two waves A1 and A2 meet each other during the wave propagation process are:

Ψ=2ACOS(ωt+φ) (where φ is the initial phase angle)

When we look at the different phase angles, what would be the result of the superposition of A1 and A2:

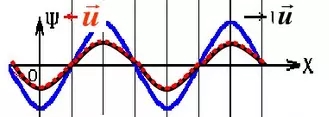
When φ=0, the waveform after superposition is as follows (blue is the superimposed waveform):

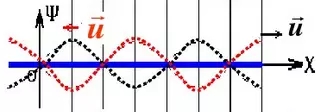
When φ=t/4, the waveform after superposition is as follows (blue is the superimposed waveform):

When φ=t/2, the waveform after superposition is as follows (blue is the superimposed waveform):

When φ=3t/4, the waveform after superposition is as follows (blue is the superimposed waveform):

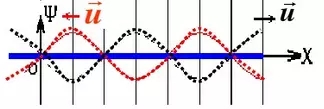
Through the above superimposed waveform, we can see that only φ = 0, A1 + A2 = 2A, that is, when the absolute value of COS (wt + φ) is equal to 1, we can get A1 + A2 = 2A, and The absolute value of COS(wt+φ) in the superposition of actual material light is always greater than zero and less than 1, ie: 0<|COS(wt+φ)|<1, further we can get: A1+A2=2A |COS(wt+φ)|, that is, 0<A1+A2<2A.

The above is the theory of LED light effect or luminous flux 1+1<2, which is explained by the volatility of light. It is purely personal and is for reference only.